By Juan Carlos Mejuto and Jesús Simal-Gándara
An artificial neural network is a mathematical prediction tool based on the reproduction of the functioning of a brain through the simulation of its basic unit, the neuron, with its ability to work together several of them, and learn from previously processed information. Each of the artificial neurons performs a very simple operation, a linear combination of the input signal (1). A neural network performs a model of approximation to the functioning of a system; hence its predictive capacity. Networks of neurons have a flexible structure and are able to establish non-linear relationships between the input and output values of the network. In addition, they can learn from real cases and re-learn when new data is introduced into the system (2-3). For example, you can make predictions in the evolution of the quality of a product (4-5), its pattern of sensory characteristics (6-7), its physicochemical characteristics, or the expected average life (8-9).
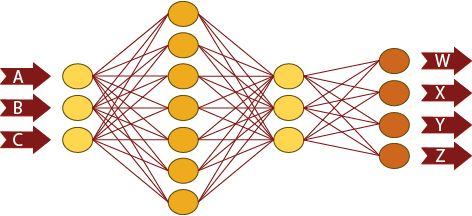
Among all known neural network architectures, the most suitable for engineering processes due to its universal approach capability is the multilayer perceptron (usually MLP, for its acronym in English) (3). This type of network consists of a layer of input neurons, an intermediate layer known as a hidden layer, and a last output layer. The neurons of the input layer collect the data of the chosen variables and introduce them into the network following an input vector. This vector propagates the information to the next layer following an activation rule that is a function of a value called weight and another known as bias. A similar calculation of weights and bias occurs in the neurons of the hidden layer, although a non-linear function is applied. At the end, an error calculation is performed at the output of the neural network. The learning algorithm is responsible for modifying the weights to minimize the value of the error in each calculation cycle. Usually the backpropagation algorithm is used, which modifies the weights of the input variables depending on the signal of the network output. If the error is acceptable, the training ends here, but otherwise the whole process is repeated. The procedure when training a neural network is to take a series of known cases and divide them into two groups. The cases are formed by the values of the input variables of the network and the known real value of the output variable. In this way, with the first group (training group) the network is trained to compare its predictions with the known real value of each case and adjust until the error is assumable. Once the training is over, the prediction capacity of the network is checked with the cases of the second group (validation group). If the training has been successful, an assumable error in the prediction of validation cases will be obtained.
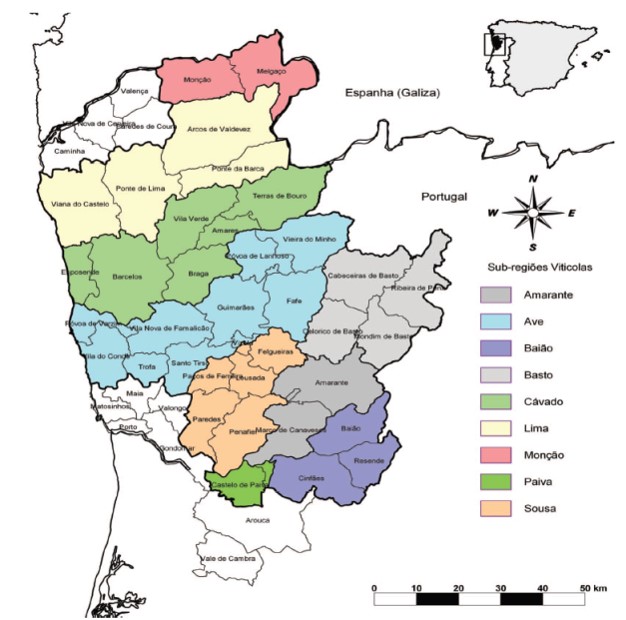
In our group, we have developed neural networks capable of predicting the type of wine produced by a red wine (10), specifically from the Green Wine Region, located in the northwest of Portugal, in an area characterized by the influence of the ocean Atlantic and a fluvial network embedded in an irregular land. There, under a mild climate of abundant rainfall, especially in winter and spring, and with the name Vinho Verde, acid red wines of low alcoholic strength are produced. Its traditional production includes the pressing of the harvest just after harvesting, and its joint fermentation of both the must and the skins, seeds and scrapes. This produces wines with high anthocyanin content, important because they give these wines their intense purple coloration, but also tend to cause over-extraction of tannins, which causes an excess of astringency on the palate. To implement the artificial neural network, we have worked with various input variables, such as the year of harvest, the clarification technique used, its absorbance at different wavelengths, the concentration of anthocyanins, some physicochemical indices or sensory variables. It is important to highlight that it is not necessary to know relationships between variables; an MLP will establish a correlation between them, which is known as a universal approximation. In this way, knowing the values for the variables of a problem wine, the network allows us to calculate what the winemaking process has been. The result has been surprising since we have obtained correlations with values of R2 greater than 0.9795, which implies that the artificial neural networks can be a valuable tool to evaluate the authenticity of the wine. In fact, neural networks are a portentous resource for multiple applications in the agro-food field (11-12).
References
- Rumelhart, D.E., McClelland, J.L., & Williams, R.J. (1986). Parallel recognition in modern computer processing: Explorations in the microstructure of cognition (Vol. 1). Cambridge: MIT Press.
- Hecht-Nielson, R. (1987). Kolmogorov’s mapping neural network existence theorem, 1st IEEE IJCNN (Vol. 3). San Diego, CA: IEEE.
Leonard, J., & Kramer, M.A. (1990). Computers and Chemical Engineering, 14, 337–341. - Ni, H., & Gunasekaran, S. (1998). Food Technology, 52, 60–65.
- Xie, G., & Xiong, R. (1999). Journal of Food Engineering, 41, 151–162.
- Park, B., Chen, Y.R., Whittaker, A.D., Miller, R.K., & Hale, D.S. (1994). Transactions of the American Society of Agricultural Engineers, 37, 1547–1553.
- Singh, R.R.B., Ruhil, A.P., Jain, D.K., Patel, A.A., & Patil, G.R. (2009). Journal of Food Engineering, 92, 146–151.
- Ko, S.H., Park, E.Y., Han, K.Y., Noh, B.S., & Kim, S.S. (2000). Food Engineering Progress, 4, 193–198.
- Vallejo-Cordoba, B., Arteaga, G.E., & Nakai, S. (1995). Journal of Food Science, 60, 885–888.
- Astray, G., Castillo, J.X., Ferreiro-Lage, J.A., J.F. Gálvez, J.C. Mejuto (2010) Journal of Food, 8, 79-86.
- Gonzalez-Fernández, I.; Iglesias-Otero, M.A.; Esteki, M.; Moldes, O.A.; Mejuto, J.C.; Simal-Gándara, J. (2018) Critical Reviews in Food Science and Nutrition, https://doi.org/10.1080/10408398.2018.1433628
- Moldes, O.A.; Mejuto, J.C.; Rial-Otero, R.; Simal-Gándara, J. (2017). Critical Reviews in Food Science and Nutrition, 13, 2896-2908.

Juan Carlos Mejuto (xmejuto@uvigo.es), Professor in the Physical Chemistry Department of University of Vigo (Spain)at Ourense Campus. He is the head of the Colloids Group at Ourense Campus. His research interest comprises (i) physical organic and physical inorganic chemistry, (ii) reactivity mechanisms in homogeneous and micro heterogeneous media, (iii) stability of self-assembly aggregates and (iv) supramolecular chemistry. Actually, he is a member of a research team working on agro-environmental sciences and food chemistry. More info at https://orcid.org/0000-0001-8396-1891

Jesus Simal-Gandara(jsimal@uvigo.es), Professor in Nutrition and Food Science at the Faculty of Food Science and Technology, University of Vigo (Spain), since 1999. He now leads a research group of excellence at NW Spain, in addition to CIA3 (Environmental, Agricultural and Food Research Center), and is the Head of the Department of Analytical Chemistry and Food Science at the University of Vigo. He performed research stays at the Université de Paris-Sud (Paris, France), University of Delaware (Newark, USA), Fraunhofer-Institut für Lebensmitteltechnologie und Verpackung (Munich, Germany), Central Science Laboratory (Norwich and York, UK), TNO-Voeding (Zeist, Netherlands), Packaging Industries Research Association (Leatherhead, UK) and The Swedish Institute for Food and Biotechnology (Gothenburg, Sweden). His focus today is on the study of persistent organic pollutants (POPs) from the point of view of public health (epidemiology, toxicity of mixtures, metabolites …), and on the study of secondary metabolites in plant foods, exploring the molecular mechanisms that explain their activity. More info at https://orcid.org/0000-0001-9215-9737

